I thought a lot about this topic recently. A few months ago I posted the growth formulas here and I will update this post soon. You see there a lot of variables. In the following just the both key factors (i.e. the Basic Growth b and the Housing Bonus h) are discussed. For simplification let us ignore truncation and let us assume that there are just Worker Units (lets denote them with w) on the planet, i.e. also no droids or natives etc. and therefore we have POPrace = POPagg = w and equation (I) in the above-mentioned blog post simplifies to:
(I) Basic Growth: b = SQRT [ 2000 * w * (POPmax - w) / POPmax ]
Let us clarify: 1 Worker Unit represents 1000k population and when the Basic Growth Rate bgr is mentioned I refer to this ratio:
(II) Basic Growth Rate: bgr = b / ( 1000 * w )
There are now 2 basic results with the current formula:
Half full planets generate the maximum Basic Growth, i.e. w = POPmax / 2 in equation (I).
But we receive the maximum Basic Growth Rate with w = 1 in equation (II).
(Be aware that we haven't considered housing yet.)
When we ignore now further bonuses (like growth picks, boom, microbiotics, leaders or cloners) we receive the total Growth tg by multiplying the Basic Growth b with the factor 1+h, where h represents the Housing Bonus:
(III) Total Growth: tg = (1 + h ) * b
and
(IV) Housing Bonus: h = Production / (2.5 * POPagg)
The Production contains the fixed Production pf (f.e. the 5 production of automated factories) and also the production caused by Worker Units. When we denote the productivity per worker with k and ignore pollution we receive:
(IVa) h = ( pf + k * w ) / (2.5 * POPagg)
Additionally, we assumed POPagg = w and (IVa) simplifies to:
(V) h (w) = (pf / 2.5) * w^(-1) + k / 2.5
Example:
An UniTolInd +1 (without any pollution)
Large abundant Terran: POPmax = 20
Autofacts and RoboMiners means pf = 15 and k = 10.5
so we have:
(I) BasicGrowth: b (w) = SQRT [ 2000 * w * ( 20 - w ) / 20 ]
(V) Housing Bonus: h (w) = 5 * w^(-1) + 4.2
and when we are housing the growth is calculated by:
Total Growth: tg (w) = [1 + 5 * w^(-1) + 4.2 ] * SQRT [ 2000 * w * ( 20 - w ) / 20 ]
Here are the results of our example (click it to enlarge):
b(w) and tg(w) under the status quo 
Surprisingly, the difference of tg (10) - tg (1) is almost completely explained by the increase in basic growth b (10) - b (1). In fact, the Housing Bonus h decreases with increasing w, i.e. the derivative
h'(w) = -5 * w^(-2)
is always below zero which is the mathematical reason why the slight increase in the Total Growth is driven by the Basic Growth.
This characterizes one part of the problem. When the first pop unit starts with housing the marginal contribution is quite big because of the fixed Production pf which is also used for housing.
So it seems to me necessary to exclude pf from the housing bonus:
(IVb) h = k * w / (2.5 * POPagg)
and again with POPagg = w we have h = k/2.5. One could argue that excluding pf makes economically sense. Improving growth is driven by government policies which are mainly based on subsidies (tax-reductions), services (kindergarten) etc. but not by the industrial complex. Housing itself seems an inapproriate expression - Childbearing (which was proposed by Cybersaber here) seems to fit better.
We receive now following results (click it to enlarge):
Pf removed 
The graphs look better, after excluding pf the bonus h is constant now (it doesnt depend on w any longer) and you receive tg(w) by multiplying the basic growth with the factor 5.2. But nevertheless 1pop-housing is still the preferred solution when you decide to use housing:
A good indicator for an efficient housing strategy should be based on the ratio of the pop-increase tg(w) - b(w) = h(w) * b(w) and the invested production units.
We need a further decision when we calculate such ratio. What should happen with the deleted pf? There are several options:
a) This Prod is simply lost.
b) It is transferred to tradegoods (which means that roundabout three quarter of the prod is lost)
c) It is simply stored.
In the following diagram you see how this deleting of pf works compared to the status quo (click it to enlarge):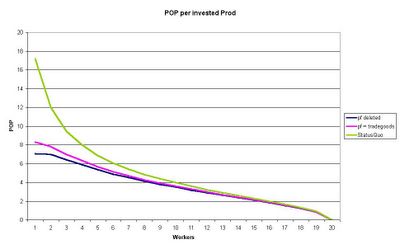
Pop per Prod 
Under the status quo 1pop housing is by far the most effective choice. 1prod generates then roundabout 17k pop. When the pf is transferred to tradegoods it decreases to 10k and when we delete this prod just 7.1k pop per prod unit are left (1pop housing). What happens when we store this production? In this case we have the same efficiency as under the status quo.
It is not quite clear which is the approriate ratio here because there is still the alternative of basic growth. We surely have to test this in several games.
Summary: Deleting pf is not enough. We need further steps. A constant bonus h might work when we have a constant basic growth rate for some interval but as pointed out above we receive the maximum basic growth rate with w = 1. (see introduction)
Further Ideas:
We could remove POPagg from the housing bonus since the negative effect of POPagg is already considered in the basic growth function. For example, when we increase the denominator in (IVb) we get:
(IVc) h = k * w / 10
The graph looks now different (click it to enlarge):
Pf and POPagg removed 
With an huge amount of prod you are then able to generate more than 1 pop unit per turn. Also the Pop per Prod ratio looks now very different (click it to enlarge):
Pop per Prod 2 
1pop housing is no longer the most effective choice. Instead of such dominant value we have now a wide range of acceptable housing decisions.
Is the maximum of 8.8k pop per prod a good value? With such a housing bonus we have a completely different game play. It is impossible to say. We need tests. I propose to test such functions with different parameters. (see below)
Does such change improve the AI? Once again. No idea at moment. I know for sure that the AI doesn't use 1pop housing systematically. When it uses housing with more than 1worker under the status quo the AI should be improved.
Further Parameters
Because of the above-mentioned difficulties it would be nice to test different housing and basic growth functions.
Instead of (IVc) I would propose a housing switch /h=a;b which determines the parameters in:
(IVd) h = ( k * w / b )^a
We receive (IVc) with the switch /h=1;10 then.
a should be a value between 0 and 1. (law of diminishing returns)
b should be positive
and instead of (I) a basic growth switch: /b=c;d;e could be useful:
(Ib) Basic Growth: b = 2000^c * {w^d * [(POPmax - w) / POPmax ]^(1-d)}^e
We receive (I) with /b=0.5;0.5;1
In this case the maximum Basic Growth is generated by w = d * POPmax
and the maximum Basic Growth rate: (e * d - 1 ) / ( e - 1 ) * POPmax
Furter, c is a good value to influence the basic growth for 1pop planets.
This should be sufficient to find a good alternative formula.
22.9.05
An alternative housing formula
Posted by siron at 1:23 pm
Labels: MOO2 formulae
Subscribe to:
Post Comments (Atom)


1 comment:
Makes total sense, even and especially from the point of view of gameplay:
1. 1-pop housing of course isn't a choice, it's the best way to use small colonies so it's a pointless mechanic as it doesn't have any negative consequence or cost
2. AI still doesn't use it after tens of patches
3. It wastes everybody's time in micro
Sad that the community, 15 years later, still hasn't matured enough to see the issue with this... Dare I use the word... Exploit!
Post a Comment